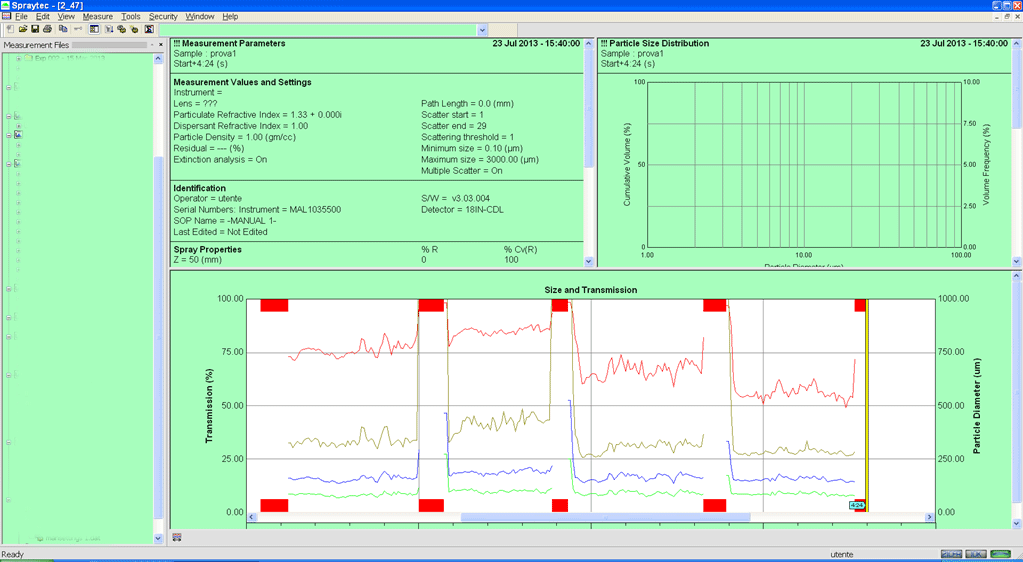
Laser Diffraction technology used by an indipendent Third-party to test performances of SPRAYTECS nozzles, as security for our customers.

Laser diffraction analysis or laser diffraction spectroscopy is a scientific technique which utilizes properties of the diffraction patterns of a laser beam passed through a substance, to measure the size of its particles.

Laser diffraction analysis is based both on the theory of Fraunhofer diffraction and on the theory of Mie scattering. 

The theory of Fraunhofer diffraction states that the intensity and angle of the light scattered by a particle is directly proportional to the size of the particle. 

When a beam of light is partly blocked by an obstacle, some of the light is scattered around the object, and light and dark bands are often seen at the edge of the shadow – this effect is known as diffraction. 

These effects can be modelled using the Huygens–Fresnel principle. Huygens postulated that every point on a primary wavefront acts as a source of spherical secondary wavelets and the sum of these secondary waves determines the form of the wave at any subsequent time.

Fresnel developed an equation using the Huygens wavelets together with the principle of superposition of waves, which models these diffraction effects quite well. 

It is not a straightforward matter to calculate the displacement given by the sum of the secondary wavelets, each of which has its own amplitude and phase, since this involves addition of many waves of varying phase and amplitude.

When two waves are added together, the total displacement depends on both the amplitude and the phase of the individual waves: two waves of equal amplitude which are in phase give a displacement whose amplitude is double the individual wave amplitudes, while two waves which are in opposite phases give a zero displacement. Generally, a two-dimensional integral over complex variables has to be solved and in many cases, an analytic solution is not available.

The Fraunhofer diffraction equation is a simplified version of the Kirchhoff's diffraction formula and it can be used to model the light diffracted when both the light source and the viewing plane are effectively at infinity with respect to the diffracting aperture. 

In this case, the incident light is a plane wave so that the phase of the light at each point in the aperture is the same. The phase of the contributions of the individual wavelets in the aperture varies linearly with position in the aperture, making the calculation of the sum of the contributions relatively straightforward in many cases.

Strictly speaking, the Fraunhofer approximation only applies when the diffracted pattern is viewed at infinity, but in practice it can be applied in the far field, and also in the focal plane of a positive lens.

When the distance between the aperture and the plane in which the pattern is observed is large enough that the difference in phase between the light from the extremes of the aperture is much less than the wavelength, then individual contributions can be treated as though they are parallel.

This is often known as the Far field and is defined as being located at a distance which is significantly greater than W²/λ, where λ is the wavelength and W is the largest dimension in the aperture. The Fraunhofer equation can be used to model the diffraction in this case.

For example, if a 0.5mm diameter circular hole is illuminated by a laser with 0.6μm wavelength, the Fraunhofer diffraction equation can be employed if the viewing distance is greater than 1000mm.

The Mie solution to Maxwell's equations (also known as the Lorenz–Mie solution, the Lorenz–Mie–Debye solution or Mie scattering) describes the scattering of electromagnetic radiation by a sphere. The solution takes the form of an analytical infinite series. 

Laser diffraction is a widely used particle sizing technique for materials ranging from hundreds of nanometers up to several millimeters in size.

The main reasons for its success are:

• Wide dynamic range - it starts from submicron to millimeters size range

• Rapid measurements - the results are generated in less than a minute.

• Repeatability - with this characteristic a large numbers of particles could be sampled in each measurement.

• Instant feedback - it is possible to monitor and to control quickly the particle dispersion process.

• High sample throughput - hundreds of measurements can be performed per day by skilled operators.

• Calibration is not necessary - because it is easily verified using standard reference materials.

• Well established technique - (ruled and covered by ISO13320 (2009).

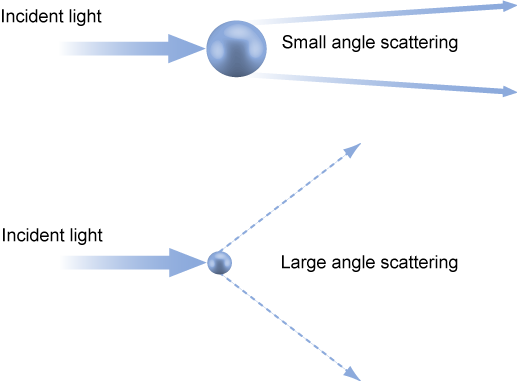
Laser diffraction measures particle size distributions by measuring the angular variation in intensity of the light scattered as a laser beam passes through a dispersed particulate sample.

Large particles scatter light at small angles relative to the laser beam and small particles scatter light at large angles, as illustrated below.

The angular scattering intensity data is then analyzed to calculate the size of the particles responsible for creating the scattering pattern, using the Mie theory of light scattering.

The particle size is reported as a volume equivalent sphere diameter.

Laser diffraction uses Mie theory of light scattering to calculate the particle size distribution, assuming a volume equivalent sphere model.

Mie theory requires knowledge of the optical properties (refractive index and imaginary component) of both the sample being measured, along with the refractive index of the dispersant.

Usually the optical properties of the dispersant are relatively easy to find from published data, and many modern instruments will have in-built databases that include common dispersants.

For samples where the optical properties are not known, the user can either measure them or estimate them using an iterative approach based upon the goodness of fit between the modeled data and the actual data collected for the sample.

Another simplified approach is to use the Fraunhofer approximation, which does not require full knowledge of the optical properties of the sample.

This can provide accurate results for large particles. Anyway it should be used with caution whenever working with samples which might have particles below 50µm or where the particles are relatively transparent.